VARDAAN LEARNING INSTITUTE | POWERED BY VARDAAN COMET

Oscillations

CBSE Class 11 Physics • Chapter 13

Chapter Overview

This chapter covers the fundamental concepts of Oscillations. Ensure you understand the definitions and derivations thoroughly.

13.1 Periodic & Oscillatory Motions

Periodic Motion: Motion that repeats itself at regular intervals of time. (e.g., Motion of planets around the Sun, Uniform Circular Motion).
Oscillatory (Vibratory) Motion: A specific type of periodic motion where the body moves to and fro (back and forth) about a fixed point called the mean position or equilibrium position.
Condition: Every oscillatory motion is periodic, but every periodic motion is not oscillatory.
Period (T): The smallest interval of time after which the motion repeats. Unit: Seconds (s).
Frequency ($\nu$ or $f$): The number of oscillations completed per unit time. $\nu = \frac{1}{T}$. Unit: Hertz (Hz) or $s^{-1}$.
Angular Frequency ($\omega$): $\omega = 2\pi\nu = \frac{2\pi}{T}$. Unit: rad/s.

Examples of Periodic Motion (a) Insect climbing wall (b) Child climbing step (c) Ball bouncing.

Periodic Functions:

Mathematical functions that repeat their values at regular intervals.

$f(t) = f(t + T)$.

Examples: $\sin \omega t$ and $\cos \omega t$ are the simplest periodic functions with period $T = 2\pi/\omega$.

Any periodic function can be expressed as a superposition of sine and cosine functions (Fourier Theorem).

NCERT Focus: Identifying Motion Types (Example 13.3)

Q: Which functions represent Periodic or SHM?

(i) $\sin \omega t - \cos \omega t$:
$= \sqrt{2} \sin(\omega t - \pi/4)$. Represents SHM with Period $2\pi/\omega$.
(ii) $\sin^3 \omega t$:
$= \frac{1}{4}(3\sin \omega t - \sin 3\omega t)$. Represents Periodic Motion but NOT SHM (it's a combo of two SHMs).
(iii) $e^{-\omega t}$:
Decreases monotonically. Represents Non-Periodic Motion.

Topic Practice: Periodic Motion

Q1: Check if $\sin^2 \omega t$ represents periodic motion. If yes, find its period.

Ans: $\sin^2 \omega t = \frac{1 - \cos 2\omega t}{2}$. It involves $\cos 2\omega t$, which is periodic.
Angular frequency is $2\omega$.
Period $T' = \frac{2\pi}{2\omega} = \frac{\pi}{\omega} = \frac{T}{2}$. Yes, it is periodic.

Q2: A human heart beats 75 times in a minute. Calculate its frequency and period.

Ans: Frequency $f = \frac{75}{60} = 1.25 \text{ Hz}$.
Period $T = \frac{1}{f} = \frac{1}{1.25} = 0.8 \text{ s}$.

13.2 Simple Harmonic Motion (SHM)

Definition: SHM is the simplest form of oscillatory motion where the restoring force is directly proportional to the displacement from the mean position and acts always towards the mean position.

$$ F = -k x $$

Where $k$ is the Force Constant (or Spring Constant). Unit: N/m.

Types of SHM:

Linear SHM: Particle oscillates along a straight line about a fixed point (e.g., Spring-Mass system). Restoring force depends on linear displacement $x$.
Angular SHM: Particle oscillates along a curved path (arc) about a fixed axis (e.g., Simple Pendulum). Restoring torque depends on angular displacement $\theta$. $\tau = -C\theta$.

Differential Equation of SHM:

From Newton's 2nd Law: $F = ma = m \frac{d^2x}{dt^2}$.

$m \frac{d^2x}{dt^2} = -kx \Rightarrow \frac{d^2x}{dt^2} + \frac{k}{m}x = 0$

Putting $\frac{k}{m} = \omega^2$, we get:

$$ \frac{d^2x}{dt^2} + \omega^2 x = 0 $$

Displacement Equation: The solution to the above DE is:

$$ x(t) = A \cos(\omega t + \phi) $$

$x(t)$: Displacement at time $t$.
$A$: Amplitude (Maximum displacement from mean position).
$(\omega t + \phi)$: Phase of the oscillator (state of motion).
$\phi$ or $\phi_0$: Phase Constant or Initial Phase (at $t=0$).

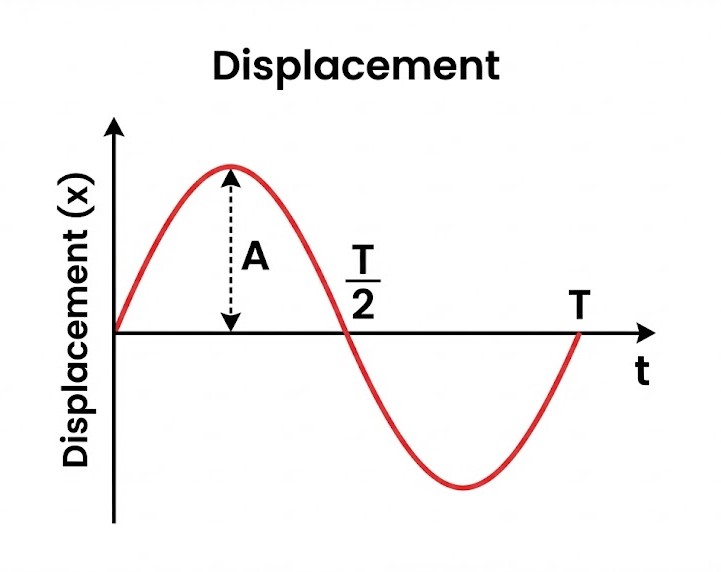
Displacement-Time Graph $x(t)$ for Simple Harmonic Motion.

Circular motion of a ball in a glass bowl (Analogy for SHM).

Geometric Interpretation of SHM (Uniform Circular Motion)

Reference Circle Method:

Simple Harmonic Motion can be visualized as the projection of Uniform Circular Motion on a diameter of the reference circle.

Reference Circle Method (P rotates, M oscillates).

Reference Particle (P): Moves on circle of radius $A$ with constant angular speed $\omega$.
Projection (M): Moves on the diameter (x-axis) executing SHM.

Coordinates of Projection M:

$x = A \cos(\omega t + \phi)$

Velocity of M: x-component of P's velocity (tangential $v=A\omega$).

$v(t) = -A\omega \sin(\omega t + \phi)$

Acceleration of M: x-component of P's acceleration (centripetal $a_c=\omega^2 A$).

$a(t) = -\omega^2 A \cos(\omega t + \phi) = -\omega^2 x$.

Topic Practice: SHM Equation

Q1: Which of the following functions of time represent (a) Simple Harmonic, (b) Periodic but not SHM, and (c) Non-periodic motion?

(i) $\sin \omega t - \cos \omega t$
(ii) $\sin^3 \omega t$
(iii) $3 \cos(\pi/4 - 2\omega t)$
(iv) $\cos \omega t + \cos 3\omega t + \cos 5\omega t$
(v) $\exp(-\omega^2 t^2)$

Ans: (i) SHM ($T=2\pi/\omega$), (ii) Periodic ($T=2\pi/\omega$), (iii) SHM ($T=\pi/\omega$), (iv) Periodic ($T=2\pi/\omega$), (v) Non-periodic.

Q2: A particle executes SHM given by $x = 5 \cos(2\pi t + \pi/4)$ in SI units. Find: amplitude, frequency, and initial phase.

Ans: Comparing with $A \cos(\omega t + \phi)$:
$A = 5 \text{ m}$
$\omega = 2\pi \Rightarrow f = 1 \text{ Hz}$
$\phi = \pi/4 \text{ rad}$.

13.3 Velocity & Acceleration in SHM

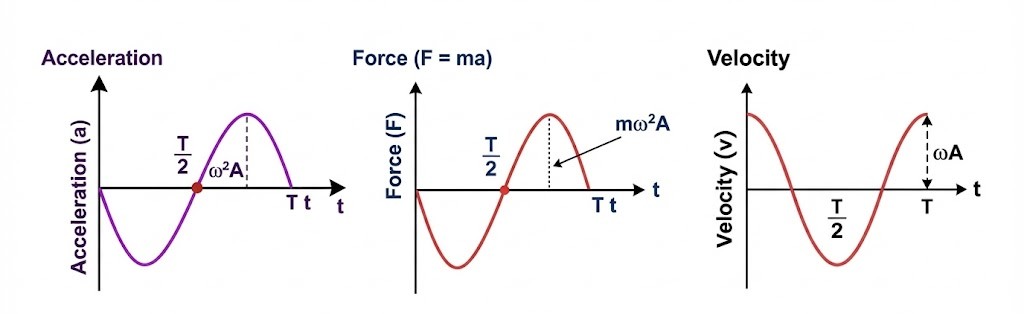
Variation of Velocity, Acceleration, and Force with Time.

1. Velocity ($v$): Rate of change of displacement.

$v = \frac{dx}{dt} = \frac{d}{dt}[A \cos(\omega t + \phi)] = -A\omega \sin(\omega t + \phi)$

Relation with $x$: Using $\sin^2\theta + \cos^2\theta = 1$

$$ v = \pm \omega \sqrt{A^2 - x^2} $$

At Mean Position ($x=0$): $v_{max} = \pm A\omega$.
At Extreme Position ($x=\pm A$): $v = 0$.

2. Acceleration ($a$): Rate of change of velocity.

$a = \frac{dv}{dt} = \frac{d}{dt}[-A\omega \sin(\omega t + \phi)] = -A\omega^2 \cos(\omega t + \phi)$

$$ a = -\omega^2 x $$

At Mean Position ($x=0$): $a = 0$.
At Extreme Position ($x=\pm A$): $a_{max} = \pm \omega^2 A$.

Topic Practice: Velocity & Acceleration

Q1 (CBSE): A particle executes SHM with amplitude $A$. At what distance from the mean position is its speed half of its maximum speed?

Ans: $v = \omega \sqrt{A^2 - x^2}$ and $v_{max} = \omega A$.
Given $v = v_{max}/2 \Rightarrow \omega \sqrt{A^2 - x^2} = \frac{\omega A}{2}$.
Squaring both sides: $A^2 - x^2 = A^2/4 \Rightarrow x^2 = 3A^2/4$.
$x = \pm \frac{\sqrt{3}}{2} A$.

Q2: Maximum velocity of a particle in SHM is $\alpha$ and maximum acceleration is $\beta$. Find the time period and amplitude.

Ans: $v_{max} = \omega A = \alpha$ ... (1)
$a_{max} = \omega^2 A = \beta$ ... (2)
Divide (2) by (1): $\omega = \beta/\alpha$.
$T = 2\pi/\omega = 2\pi \alpha / \beta$.
From (1): $A = \alpha / \omega = \alpha / (\beta/\alpha) = \alpha^2 / \beta$.

13.4 Force Law & Spring Systems

Linear Simple Harmonic Oscillator: A system oscillating under a restoring force $F = -kx$.

Time Period: $T = 2\pi \sqrt{\frac{m}{k}}$.

Frequency: $\nu = \frac{1}{2\pi} \sqrt{\frac{k}{m}}$.

(a) Block attached to spring (displaced). (b) Displacement-time graph.

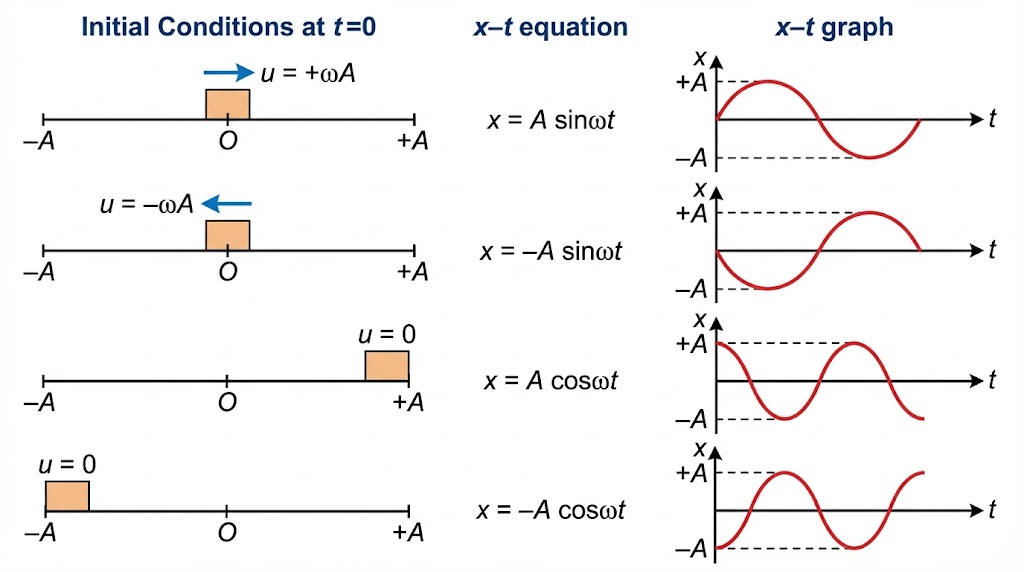
Initial Conditions determining $x(t)$ equation and graph.

Vertical Oscillations of a Spring:

Figure: Vertical Spring System in Unstretched, Equilibrium, and Displaced states.

Equilibrium Position: Weight balances spring force.

$k l_0 = mg$ (where $l_0$ is extension at equilibrium).

Displaced Position: Pulled down by distance $y$.

Total extension = $l_0 + y$.

Restoring Force $F = mg - k(l_0 + y)$.

$F = mg - k l_0 - ky$. (Since $mg = k l_0$).

$F = -ky$.

This is SHM condition. Thus, Time Period is same as horizontal spring:

$$ T = 2\pi \sqrt{\frac{m}{k}} $$

Combinations of Springs:

1. Springs in Parallel: (Both springs pulled by deduction)

Figure: Springs in Parallel (Side-by-side).

If two springs $k_1$ and $k_2$ are connected such that extension ($x$) is same for both.

$F_{total} = F_1 + F_2 = -(k_1 x) - (k_2 x) = -(k_1 + k_2)x$.

$$ k_{eq} = k_1 + k_2 $$

$T_{par} = 2\pi \sqrt{\frac{m}{k_1 + k_2}}$.

2. Springs in Series: (End to end)

Figure: Springs in Series (End-to-End).

Force $F$ is same in both springs. Extensions are $x_1$ and $x_2$. Total extension $x = x_1 + x_2$.

$x_1 = -F/k_1$, $x_2 = -F/k_2$.

$x = -F(\frac{1}{k_1} + \frac{1}{k_2})$. Also $x = -F/k_{eq}$.

$$ \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} $$

$T_{ser} = 2\pi \sqrt{m(\frac{1}{k_1} + \frac{1}{k_2})} = 2\pi \sqrt{\frac{m(k_1+k_2)}{k_1 k_2}}$.

Topic Practice: Spring Systems

Q1: Two identical springs of spring constant $k$ are attached to a block of mass $m$ and to fixed supports as shown. (a) Series (b) Parallel. Find the ratio of their Time Periods.

Ans: (a) Series: $k_{eq} = k/2$. $T_s = 2\pi \sqrt{2m/k}$.
(b) Parallel: $k_{eq} = 2k$. $T_p = 2\pi \sqrt{m/2k}$.
Ratio $T_s / T_p = \sqrt{2}/\sqrt{1/2} = \sqrt{4} = 2:1$.

Q2: A spring with force constant $k$ is cut into two equal halves. What is the spring constant of each half?

Ans: Spring constant is inversely proportional to length ($k \propto 1/L$).
If length becomes $L/2$, force constant becomes $2k$. So, each half has stiffness $2k$.

13.5 KE, PE and TE in SHM

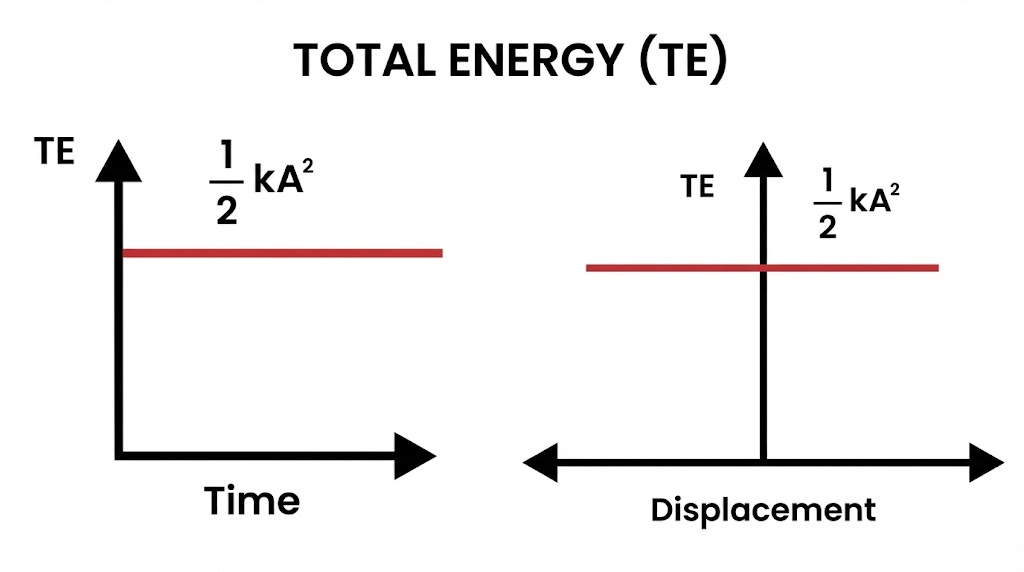
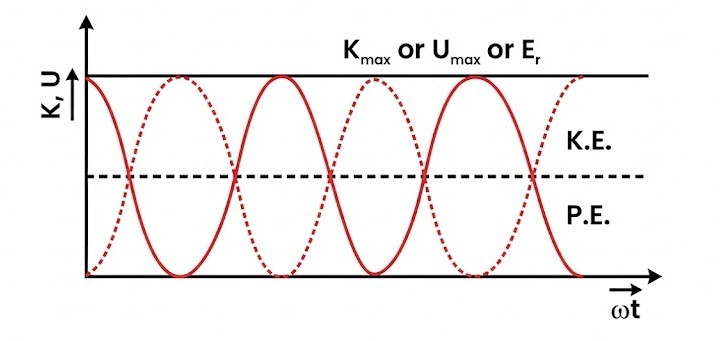
Combined Plot of Kinetic, Potential, and Total Energy.

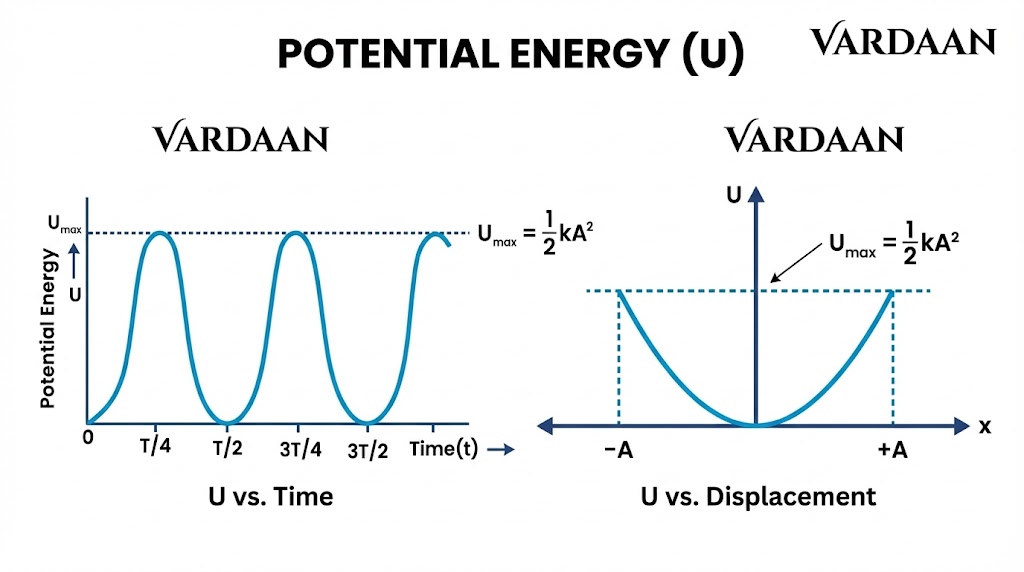
1. Potential Energy ($U$): Work done against restoring force $F = -kx$.

$dW = -F dx = -(-kx)dx = kx dx$.

$U = \int_0^x kx' dx' = \frac{1}{2} k x^2$.

Using $x = A \cos(\omega t + \phi)$:

$$ U = \frac{1}{2} m \omega^2 A^2 \cos^2(\omega t + \phi) $$

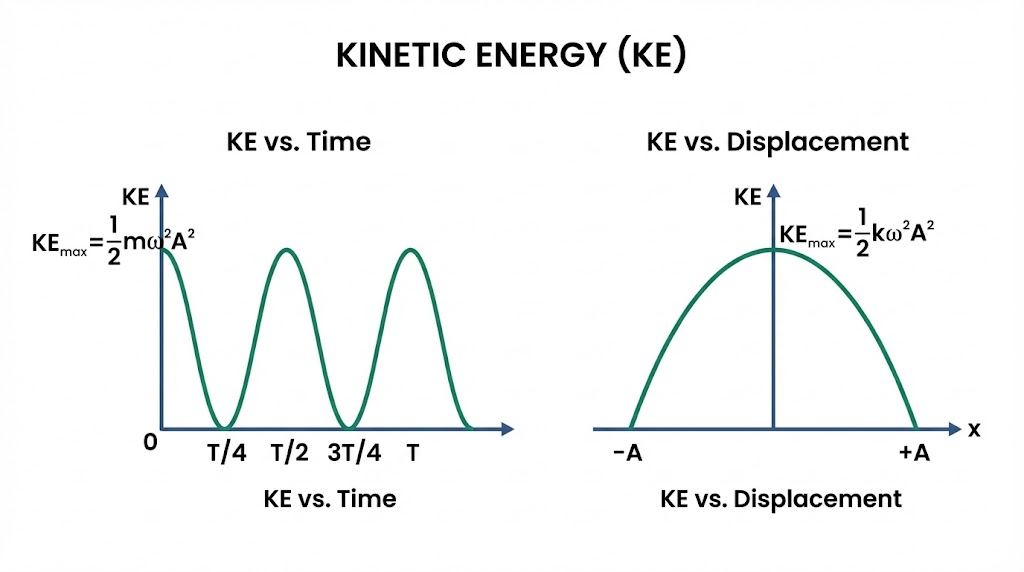
2. Kinetic Energy ($K$): $K = \frac{1}{2} m v^2$.

Using $v = -A\omega \sin(\omega t + \phi)$:

$$ K = \frac{1}{2} m \omega^2 A^2 \sin^2(\omega t + \phi) $$

3. Total Mechanical Energy ($E$):

$E = K + U = \frac{1}{2} m \omega^2 A^2 (\sin^2 \theta + \cos^2 \theta)$.

$$ E = \frac{1}{2} k A^2 = \text{Constant} $$

At Mean Position ($x=0$): $U=0, K=E$. At Extreme ($x=\pm A$): $U=E, K=0$.

Topic Practice: Energy in SHM

Q1: At what position from the mean is the Potential Energy equal to half the Total Energy?

Ans: $U = E/2 \Rightarrow \frac{1}{2} k x^2 = \frac{1}{2} (\frac{1}{2} k A^2)$.
$x^2 = A^2/2 \Rightarrow x = \pm A/\sqrt{2}$.

Q2: Plot the graph of Potential Energy and Kinetic Energy with respect to time for one complete oscillation.

Hint: Use the graph provided in figure. Note that PE is max at extremes (t=T/4, 3T/4) and KE is max at mean (t=0, T/2, T).

13.6 The Simple Pendulum

Forces acting on a Simple Pendulum

Derivation:

1. Forces acting on bob: Tension $T$ (along string) and Weight $mg$ (downwards).

2. Resolve $mg$: along string ($mg \cos\theta$) and perpendicular ($mg \sin\theta$).

3. Restoring force acts towards mean position: $F_{res} = -mg \sin\theta$.

4. For small angles ($\theta < 10^\circ$), $\sin\theta \approx \theta$ (in radians). And $\theta=\frac{\text{arc}}{\text{radius}}=\frac{x}{L}$.

5. $F_{res} = -mg \frac{x}{L}$.

6. Comparing with $F = -kx$, we get effective spring constant $k_{eff} = \frac{mg}{L}$.

Time Period:

$T = 2\pi \sqrt{\frac{m}{k_{eff}}} = 2\pi \sqrt{\frac{m}{mg/L}}$

$$ T = 2\pi \sqrt{\frac{L}{g}} $$

Seconds Pendulum: A pendulum whose period is 2 seconds. Length $L \approx 1 \text{ m}$ (on Earth).

Simple Pendulum showing Equilibrium and Extreme Positions.

Physical Pendulum (Compound Pendulum)

A rigid body oscillating about a horizontal axis passing through it at some distance from the center of mass.

Time Period:

$$ T = 2\pi \sqrt{\frac{I}{mgl}} $$

$I$: Moment of Inertia about the axis of rotation ($I = I_{CM} + ml^2$).
$m$: Mass of the body.
$l$: Distance between center of mass and pivot point.

Topic Practice: Simple Pendulum

Q1: A simple pendulum has a time period $T_1$ on Earth ($g=9.8$). It is taken to the Moon where $g_{moon} = g/6$. What is the new time period?

Ans: $T \propto 1/\sqrt{g}$.
$T_{moon}/T_{earth} = \sqrt{g_{earth} / g_{moon}} = \sqrt{g / (g/6)} = \sqrt{6}$.
$T_{moon} = \sqrt{6} T_1 \approx 2.45 T_1$.

Q2: What is the length of a "Seconds Pendulum" ($T=2s$) on Earth?

Ans: $T = 2\pi \sqrt{L/g} \Rightarrow T^2 = 4\pi^2 L/g$.
$L = g T^2 / 4\pi^2 = (9.8 \times 4) / (4 \times 9.86) \approx 0.993 \approx 1 \text{ meter}$.

Q3: A pendulum is suspended in a lift moving up with acceleration $a$. How does the Time Period change?

Ans: Effective gravity becomes $g_{eff} = g + a$.
$T = 2\pi \sqrt{L / (g+a)}$. The time period decreases (oscillates faster).

13.7 Damped & Forced Oscillations

1. Free Oscillation: Oscillation under internal restoring force only. Amplitude remains constant (Undamped).

2. Damped Oscillation: Amplitude decreases with time due to resistive forces.

Equation: $m \frac{d^2x}{dt^2} + b \frac{dx}{dt} + kx = 0$ ($b$ is damping constant).

Amplitude Decay: $A(t) = A_0 e^{-bt/2m}$.

Types of Damping:

Overdamped: Returns to equilibrium without oscillating (slowly). Large damping.
Critically Damped: Returns to equilibrium as quickly as possible without oscillating. (Used in car shock absorbers).
Underdamped: Oscillates with decreasing amplitude (Most common case).

Figure: Damped Harmonic Motion (Amplitude decays exponentially).

3. Forced Oscillation: Driven by external periodic force $F(t) = F_0 \cos(\omega_d t)$.

Equation of Motion:

$$ m\frac{d^2x}{dt^2} + b\frac{dx}{dt} + kx = F_0 \cos(\omega_d t) $$

Resonance: When driving frequency matches natural frequency ($\omega_d \approx \omega_n$).

Amplitude becomes maximum: $A_{max} \approx \frac{F_0}{b\omega}$. Sharp resonance occurs for small damping $b$.

Figure: Resonance Curve showing variation of Amplitude with Driving Frequency.

Resonance Curve

Topic Practice: Damped & Forced

Q1: What is the effect of damping on the amplitude and frequency of an oscillator?

Ans: Amplitude decreases exponentially with time: $A(t) = A_0 e^{-bt/2m}$.
Frequency decreases slightly: $\omega' = \sqrt{k/m - (b/2m)^2}$.

Q2: Distinguish between Free, Force, and Resonant Oscillations.

Ans: (1) Free: Vibrates with natural frequency, no external force.
(2) Forced: Driven by external periodic force, vibrates with frequency of driver.
(3) Resonance: Special case of forced oscillation where Driver Frequency = Natural Frequency. Amplitude is maximum.

13.8 Important Definitions

Epoch (Initial Phase): The phase at $t=0$ ($\phi$). It determines the starting position and direction of motion.
Restoring Force: Detailed as the force that brings the body back to equilibrium. $F \propto -x$.
Mechanical Energy Conservation: Total energy ($K+U$) in SHM (undamped) is constant and independent of time.

13.9 Solved Examples

Example 1: Displacement Equation

Q: A body oscillates with SHM according to the equation $x = 5 \cos(2\pi t + \pi/4)$. Find (a) Amplitude, (b) Time Period, (c) Initial Phase.

Sol: Compare with $x = A \cos(\omega t + \phi)$.

(a) $A = 5 \text{ m}$ (assuming SI).

(b) $\omega = 2\pi$. Since $\omega = 2\pi/T \Rightarrow 2\pi/T = 2\pi \Rightarrow T = 1 \text{ s}$.

Example 2: Spring System

Q: A mass of 2kg is attached to a spring of constant $k = 200 \text{ N/m}$. Calculate the frequency of oscillation.

Sol: $m = 2 \text{ kg}$, $k = 200 \text{ N/m}$.

$\nu = \frac{1}{2\pi} \sqrt{\frac{k}{m}} = \frac{1}{2\pi} \sqrt{\frac{200}{2}} = \frac{1}{2\pi} \sqrt{100} = \frac{10}{2\pi} \approx 1.59 \text{ Hz}$.

Example 3: Pendulum Change

Q: The length of a simple pendulum is increased by 44%. What is the percentage increase in its time period?

Sol: $T \propto \sqrt{L}$. Let initial length be $L$. New length $L' = L + 0.44L = 1.44L$.

$T' \propto \sqrt{1.44L} = 1.2 \sqrt{L} = 1.2 T$.

Increase $= T' - T = 0.2T$.

% Increase $= \frac{0.2T}{T} \times 100 = 20\%$.

13.10 Practice Questions

[Conceptual] Can a motion be periodic but not oscillatory? Give an example.
[Conceptual] At what points is the velocity of a particle in SHM zero?
[Numerical] A body executes SHM with an amplitude of 10 cm and a period of 4 s. Find the speed at 5 cm from the mean position.
[Numerical] Two springs of constants $k_1$ and $k_2$ are connected in series. Derive the expression for the effective spring constant.
[Long Answer] Prove that the total mechanical energy of a particle executing simple harmonic motion is conserved. Plot the graphs of KE and PE.
[Derivation] Show that the motion of a simple pendulum is simple harmonic for small angles of oscillation.

Master Strategy: For SHM problems, always identify $\omega$ first. Most quantities ($v, a, T, K, U$) depend on $\omega$. Remember $\omega = \sqrt{k/m}$ for springs and $\omega = \sqrt{g/L}$ for pendulums.