Circles

Created by Team Vardaan with ❤️

1. Definition & Basics

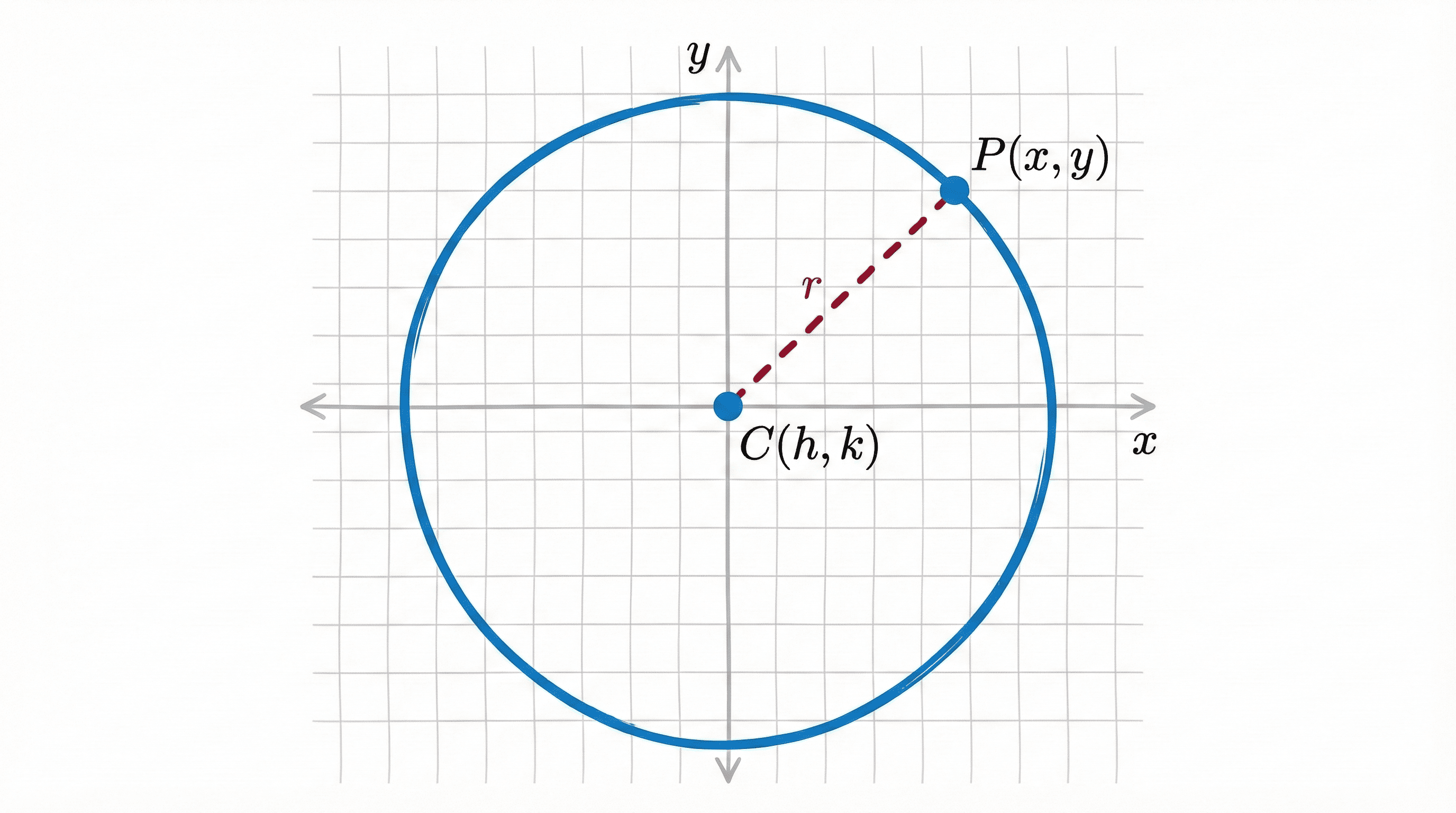
Definition

A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.

Fixed Point: Center ($C$)
Constant Distance: Radius ($r$)

Figure 1: Basic Circle Geometry showing Center C, Point P, and Radius r

2. Equations of a Circle

A. Central Form (Standard Form)

If the center of the circle is $(h, k)$ and the radius is $r$:

$$ (x - h)^2 + (y - k)^2 = r^2 $$

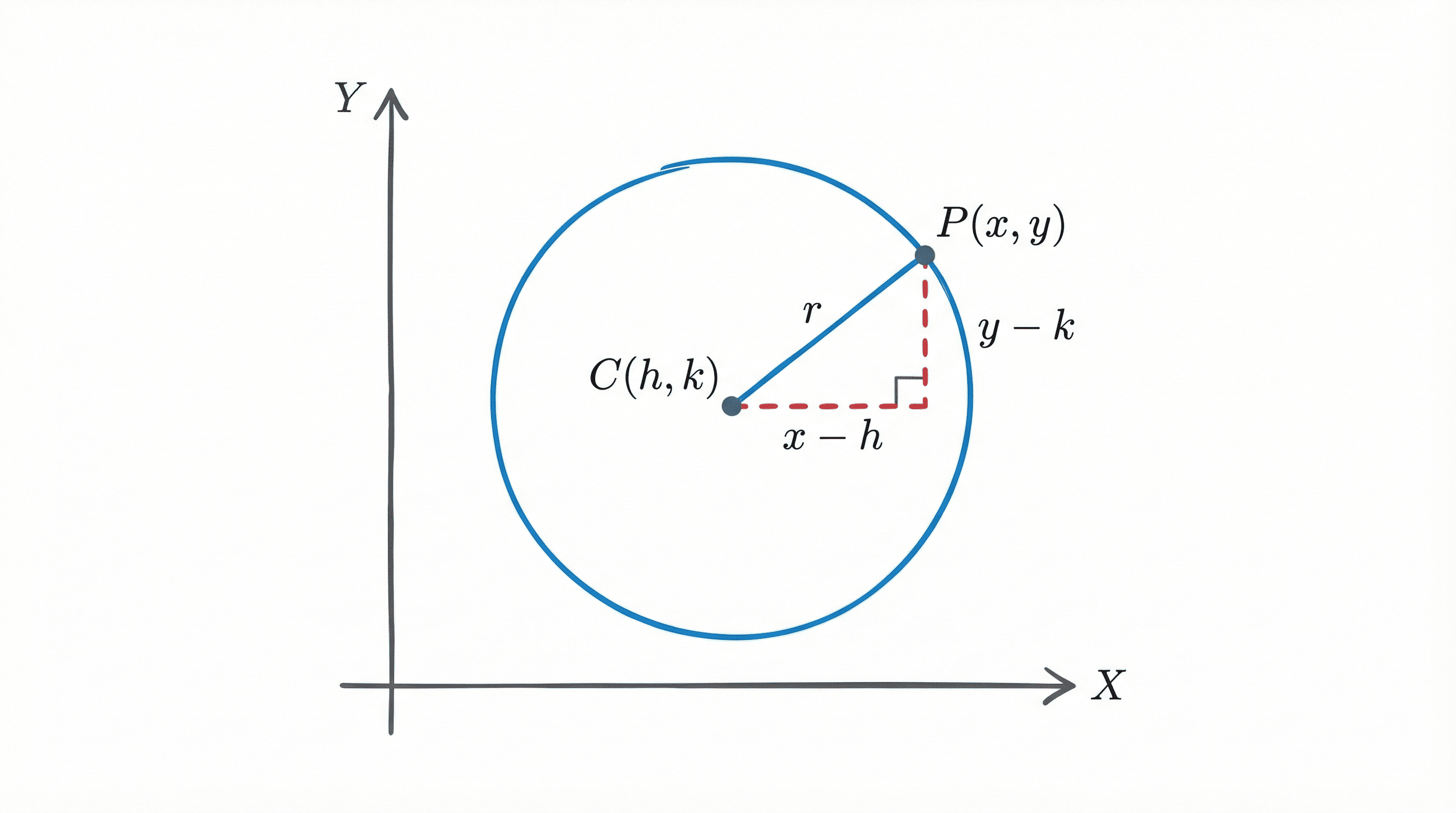
Figure 2.1: Central Form Derivation

Proof / Derivation

Let $P(x, y)$ be any point on the circle and $C(h, k)$ be the center.

By definition, the distance $CP = r$.

Using the Distance Formula:

$$ \sqrt{(x - h)^2 + (y - k)^2} = r $$

Squaring both sides gives the standard equation:

$$ (x - h)^2 + (y - k)^2 = r^2 $$

B. Simplest Form

If the center is at the origin $(0, 0)$ and radius is $r$, the equation simplifies to:

$$ x^2 + y^2 = r^2 $$

C. General Equation

The general equation of second degree representing a circle is:

$$ x^2 + y^2 + 2gx + 2fy + c = 0 $$

Figure 2.2: General Equation Parameters

Derivation from Standard Form

Expand the standard equation $(x - h)^2 + (y - k)^2 = r^2$:

$x^2 - 2hx + h^2 + y^2 - 2ky + k^2 = r^2$

$x^2 + y^2 + (-2h)x + (-2k)y + (h^2 + k^2 - r^2) = 0$

Comparing this with the general form:

$2g = -2h \Rightarrow h = -g$ (Center x-coordinate)
$2f = -2k \Rightarrow k = -f$ (Center y-coordinate)
$c = h^2 + k^2 - r^2$

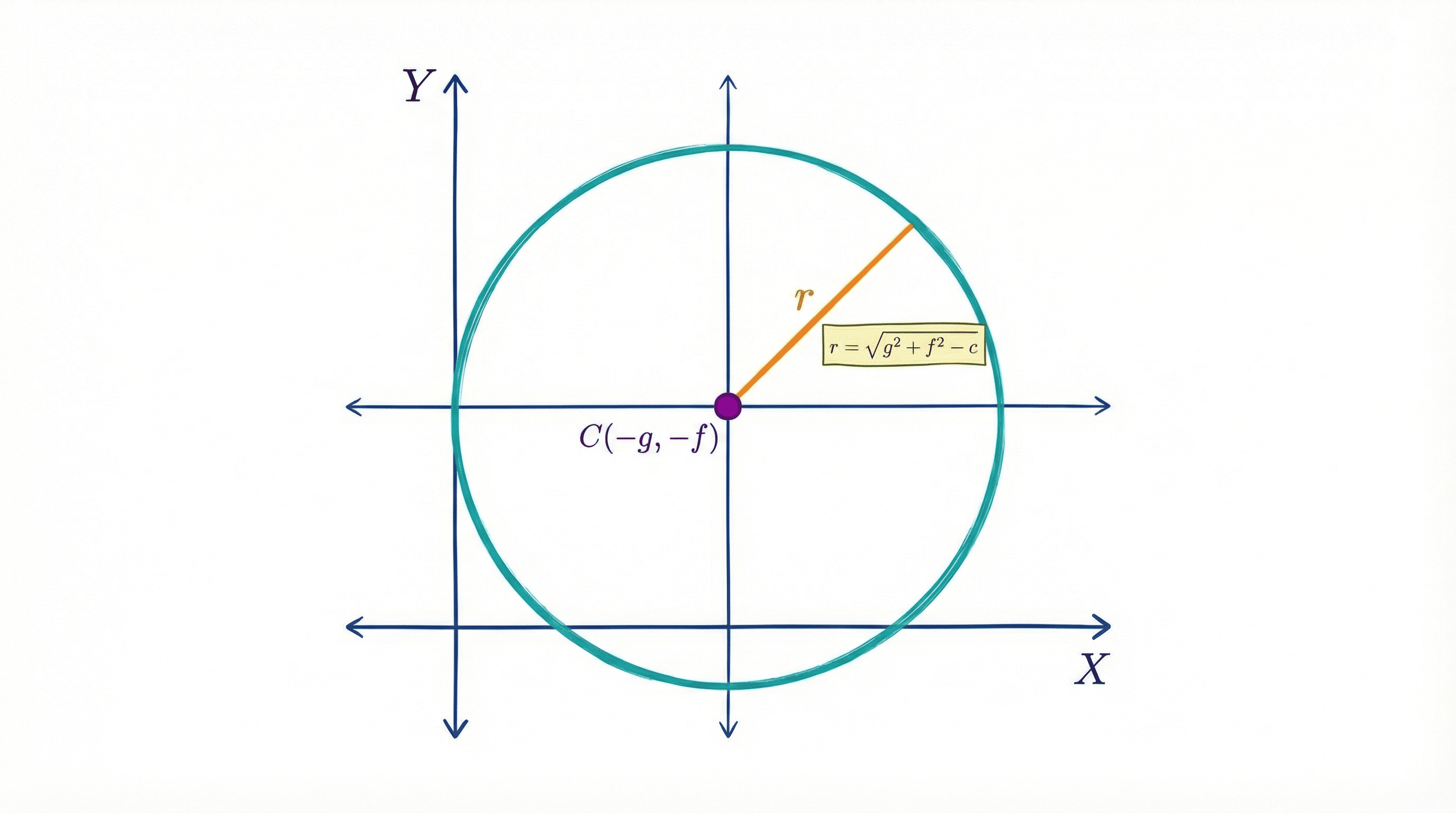
            Key Parameters
            Center: $(-g, -f)$
Radius: $r = \sqrt{g^2 + f^2 - c}$

        

Master Tip: Always ensure the coefficients of $x^2$ and $y^2$ are 1 before finding the Center and Radius. If the equation is $2x^2 + 2y^2 + \dots$, divide the entire equation by 2 first!

Nature of Circle

Check the value of $r^2 = g^2 + f^2 - c$:

$> 0$: Real Circle (Real radius)
$= 0$: Point Circle (Radius is 0, circle shrinks to a point)
$< 0$: Imaginary Circle (No real locus exists)

D. Diameter Form

Use this when coordinates of the diameter endpoints $A(x_1, y_1)$ and $B(x_2, y_2)$ are given.

$$ (x - x_1)(x - x_2) + (y - y_1)(y - y_2) = 0 $$

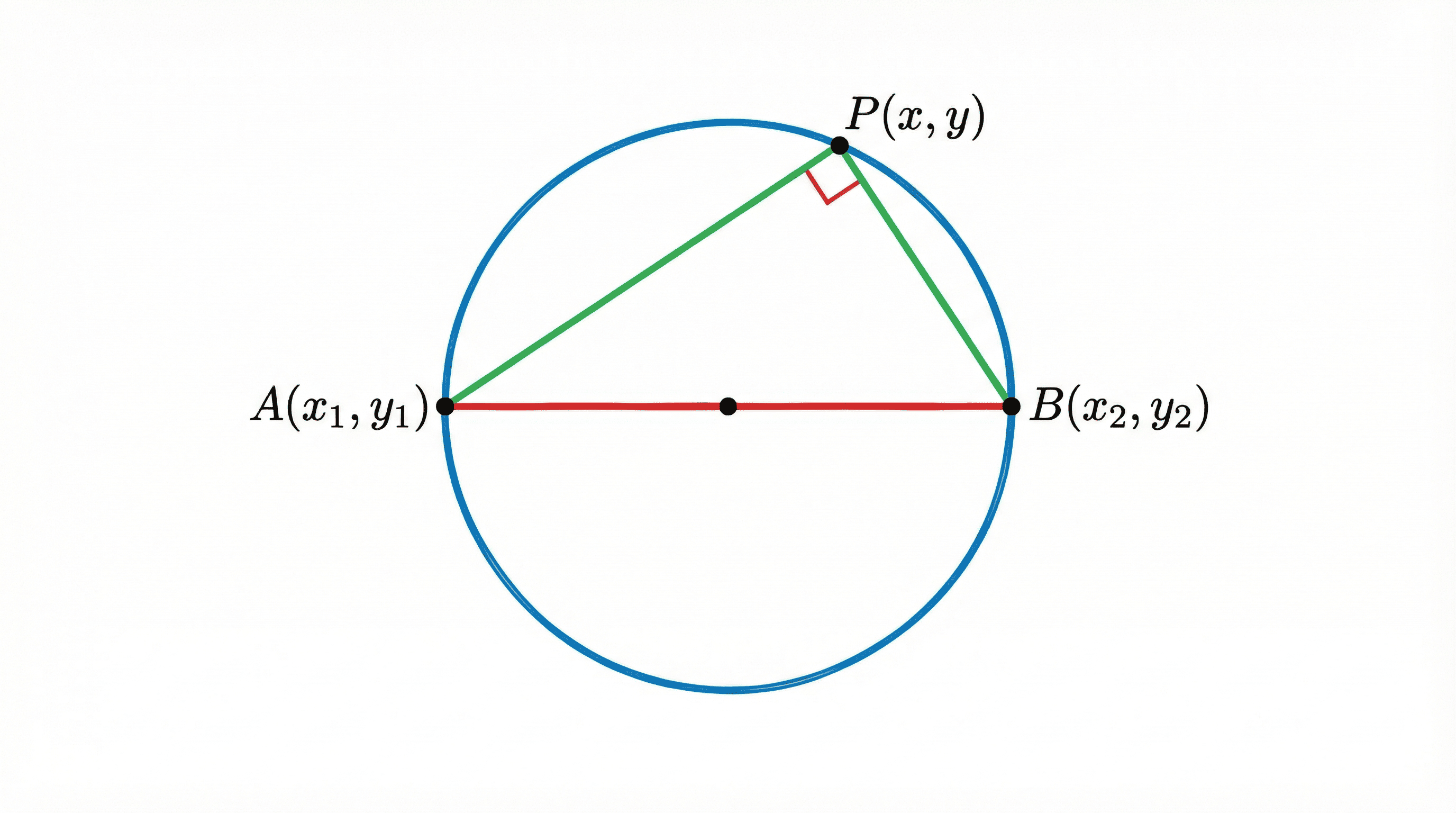
Figure 2.3: Angle in Semicircle is 90°

Proof Logic

Angle in a semi-circle is a right angle ($90^\circ$).

Let $P(x, y)$ be any point on the circle. Lines $AP$ and $BP$ are perpendicular.

Product of their slopes $m_1 \times m_2 = -1$:

$$ \left(\frac{y - y_1}{x - x_1}\right) \cdot \left(\frac{y - y_2}{x - x_2}\right) = -1 $$

Rearranging terms gives the diameter form equation.

E. Parametric Form

For a circle with center $(h, k)$ and radius $r$, the parametric coordinates are:

$$ x = h + r \cos \theta $$ $$ y = k + r \sin \theta $$

where $\theta$ is the parameter ($0 \le \theta < 2\pi$).

3. Geometric Properties

A. Position of a Point

To check where a point $P(x_1, y_1)$ lies with respect to the circle $S \equiv x^2 + y^2 + 2gx + 2fy + c = 0$.

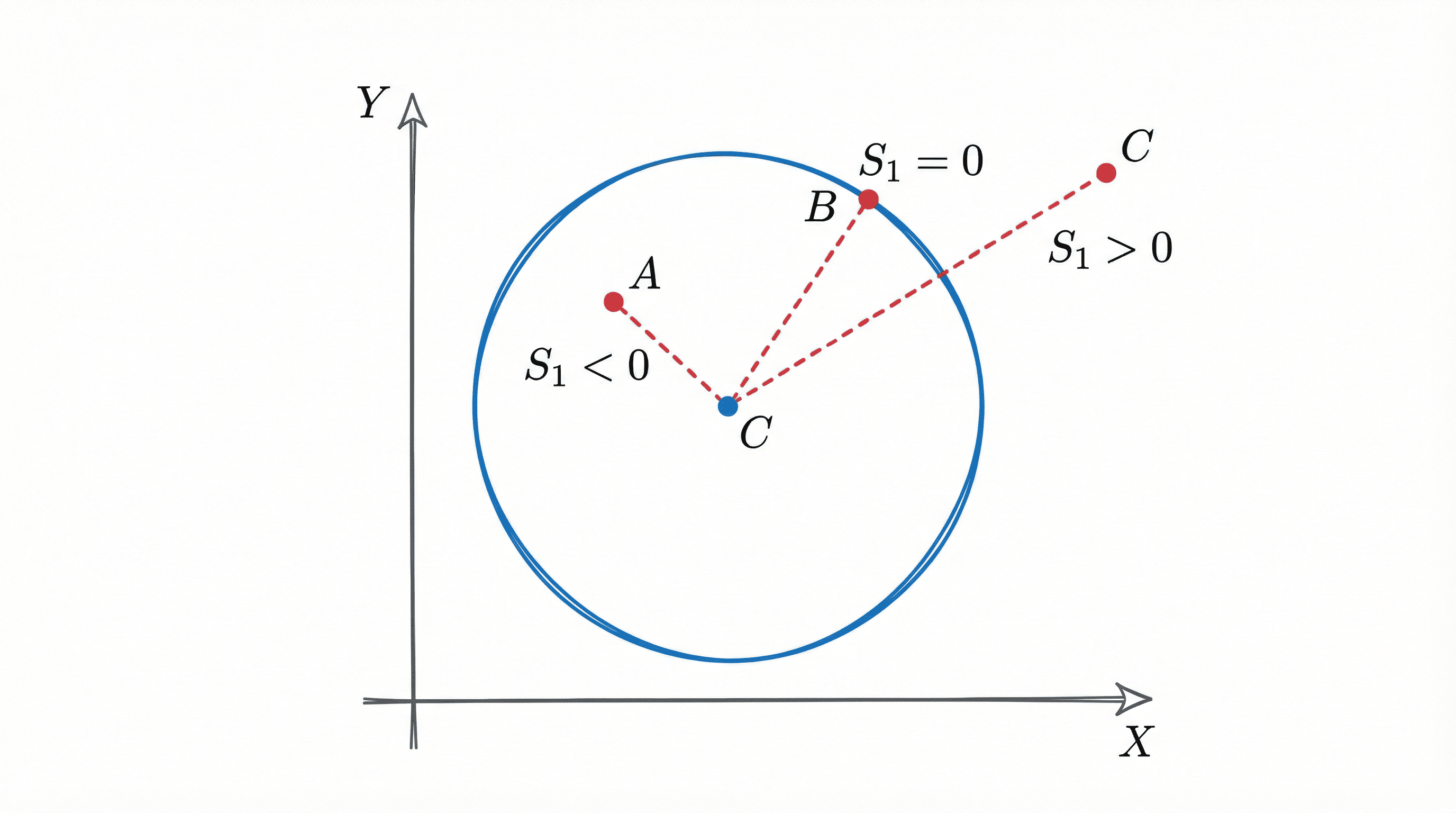
Rule: Power of Point ($S_1$)

Substitute the point coordinates into the equation:

$$ S_1 = x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c $$

$S_1 > 0 \Rightarrow$ Point is Outside ($CP > Radius$)
$S_1 = 0 \Rightarrow$ Point is On the circle ($CP = Radius$)
$S_1 < 0 \Rightarrow$ Point is Inside ($CP < Radius$)

Figure 3.1: Relative Positions of Points

B. Line and Circle Interaction

Let $d$ be the perpendicular distance from the Center to the line, and $r$ be the radius.

                    $d > r$: Line does not intersect (No common points).
$d = r$: Line is a Tangent (Touches at 1 point).
$d < r$: Line is a Secant (Cuts at 2 points).

                

C. Intercepts on Axes

If a circle cuts the coordinate axes, the lengths of intercepts are given by:

Axis	Length Formula	Condition to Cut
X-Axis	$2\sqrt{g^2 - c}$	$g^2 > c$
Y-Axis	$2\sqrt{f^2 - c}$	$f^2 > c$

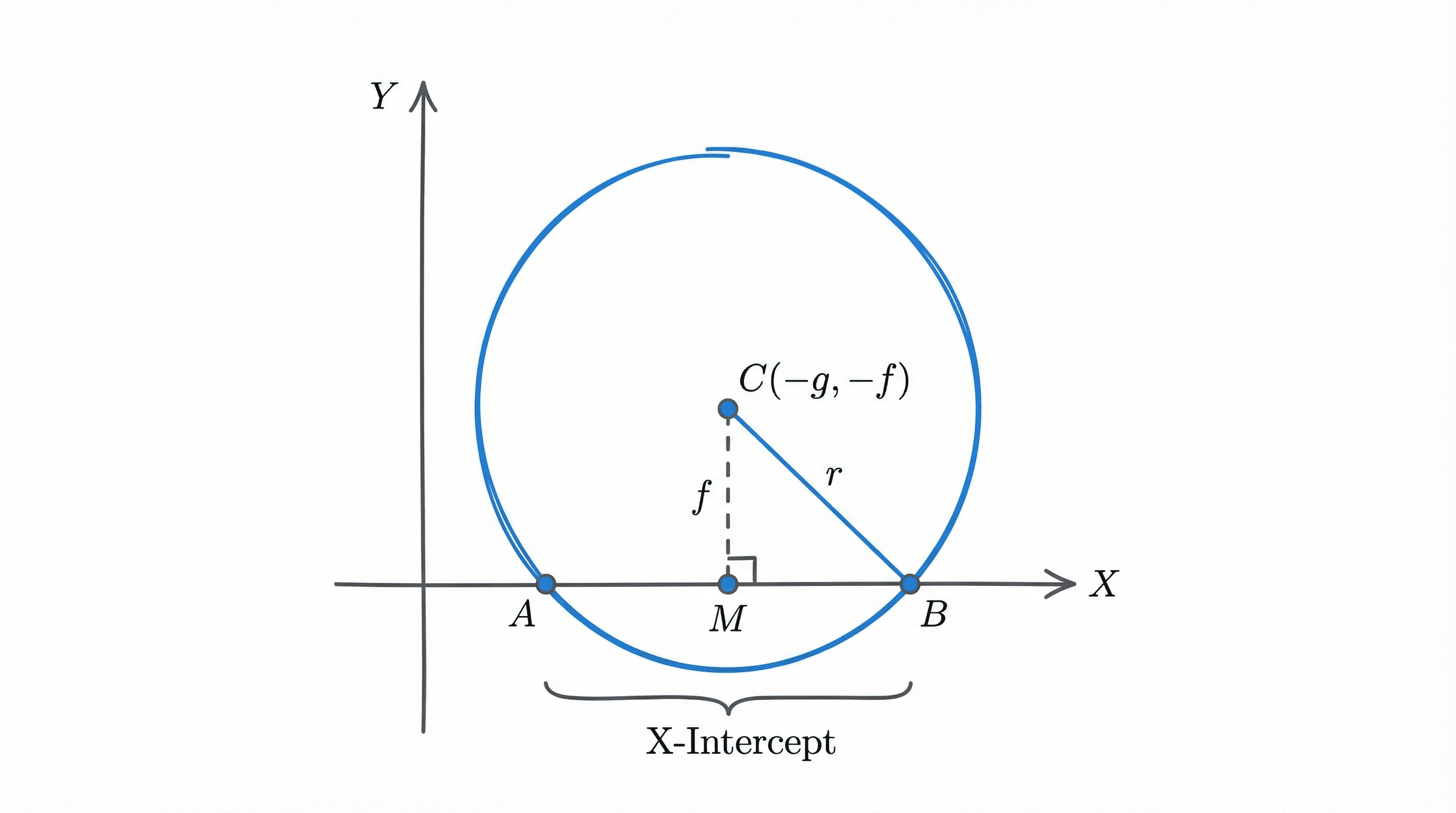
Figure 3.2: X-Intercept Geometry

Derivation (X-Intercept)

1. Center $C(-g, -f)$. Perpendicular distance to X-axis is $|-f| = f$.

2. In right $\Delta CMA$ ($M$ is midpoint of chord): $CA = r$, $CM = f$.

3. By Pythagoras: $AM = \sqrt{r^2 - f^2} = \sqrt{(g^2+f^2-c) - f^2} = \sqrt{g^2-c}$.

4. Total intercept $AB = 2 \times AM = 2\sqrt{g^2 - c}$.

Quick Recap

Form	Equation	Key Features
Standard	$(x-h)^2 + (y-k)^2 = r^2$	Center $(h,k)$, Radius $r$
General	$x^2+y^2+2gx+2fy+c=0$	$C(-g,-f)$, $r=\sqrt{g^2+f^2-c}$
Diameter	$(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = 0$	Endpoints $(x_1,y_1), (x_2,y_2)$